자료구조 - 세그먼트 트리

요즘 재밌게 풀고 있는 주제가 세그먼트 트리이다.

 

아마 다들 이 문제로 처음 세그먼트 트리를 접했을 것이다. 이 문제는 세그먼트 트리를 사용해서 구간의 최솟값을 O(log N)만에 구하는 문제이다. 이처럼 세그먼트 트리는 구간에 대한 질의(Query)를 최적화하는 방법들 중 하나이다. 공부중인 Mo's Algorithm이나 Sqrt Decomposition과 함께 응용되어 사용되기도 하고 여러가지 형태로 변형되어 무궁무진하게 쓰이는 자료구조이다. 이런 이유로 내가 굉장히 재밌어하는 부분이 있다.

 

세그먼트 트리의 개념은 완전 이진 트리 형태로 구간질의를 최적화 하는 방법으로, 각각의 리프 노드를 길이 1짜리 구간, 그리고 내부 노드는 자식 둘의 구간을 합친 구간에 대한 답으로 구현한다. 예를 들어 수열과 쿼리 17 문제처럼 최솟값을 구한다 하면 내보 노드는 자식 둘의 구간의 최솟값을 담고 있고, 이는 자식 둘이 담고 있는 값들의 최솟값과 같다.

이처럼 분할 정복과 유사하게 구간을 둘로 쪼개 질의를 진행하고 그 결과들을 토대로 원하는 구간의 질의를 수행하는 방식이 가능하면, 세그트리로 효율적으로 문제를 풀 수 있다.

 

이론에 대한 더 자세한 내용은 라이님 블로그나 BOJ Book을 참고하자. BOJ Book이 은근히 설명도 좋고 예시 시뮬레이션도 할 수 있고 예제도 많이 담고 있어 유용하다.

 

그래서 이 세그먼트 트리를 어떤 식으로 응용하는지 알아보자. 보통 수열과 쿼리를 뒤져보다 보면 세그먼트 트리 태그랑 이상한 알고리즘분류가 같이 붙어있는 경우를 볼 수 있다. 꼭 그렇지 않더라도, 세그먼트 트리만 있는데 난이도가 비정상적으로 높은 경우도 있다. 이런 식으로 세그트리가 응용되는 것들을 찾아보았다.

가장 기본적으로 구간 최솟/최댓값, 구간 합 등을 각각 일차원적인 min, max, + 연산을 통해 구할 수 있다. 이는 기본적인 형태의 세그먼트 트리 적용예시라고 볼 수 있다. 이정도는 solvedac 난이도 골드1~플래5 정도로, 이후에 설명할 문제들에 비해 난이도는 낮은 편이다.

 

다음으로, 구간 합 구하기를 봤다면, 구간 합 구하기 2도 봤을 것이다. 여기선 lazy 정보을 이용해서 느리게 갱신되는 세그먼트를 구현한 것으로, 구간 값 변화를 효율적으로 수행할 수 있다. 뭐 1~7 구간에 일괄적으로 5를 더한다던가 하는 것 말이다.

 

여기까지는 그래도 BOJ Book에 느갱세그도 설명되어 있기도 하고 어떤 새로운 자료구조를 배우는 느낌이지만, 이제는 아니다. 

https://www.acmicpc.net/problem/17408

17408번: 수열과 쿼리 24

이 문제를 보자. 이 문제는 다른 알고리즘 필요 없이 세그먼트 트리로만 풀 수 있는 문제이다. 문제의 요지는 구간에서 두개의 합의 최댓값, 달리 말하면 구간에서 최댓값 두개를 구해오라는 문제이다.

 

단적으로 생각해보면 구간의 최댓값을 구하고 그걸 빼고 남은 두 구간을 한번 더 돌리면 되지 않을까? 라는 풀이가 나올 수 있다. 하지만 그정도 응용으로는 부족하다. 세그먼트 트리의 핵심 개념인 두 소구간에 대한 정보만으로 원하는 구간의 정보를 알아내야 한다는 점인데, 이 방법은 두 구간의 정보 중 최댓값이 나오지 않는 구간에 대한 정보를 사용하지 않고 있어서 비효율적이다.

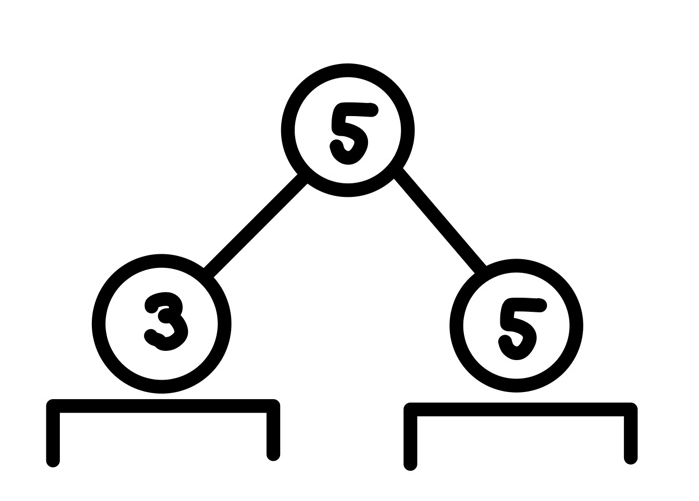
그림으로 설명하자면 여기서 전체 구간의 다음 최댓값이 3이 될 수도 있기 때문이다. 그렇다면 어떻게 해야 할까? 답은 구간에 최댓값을 두개씩 담는 것이다.

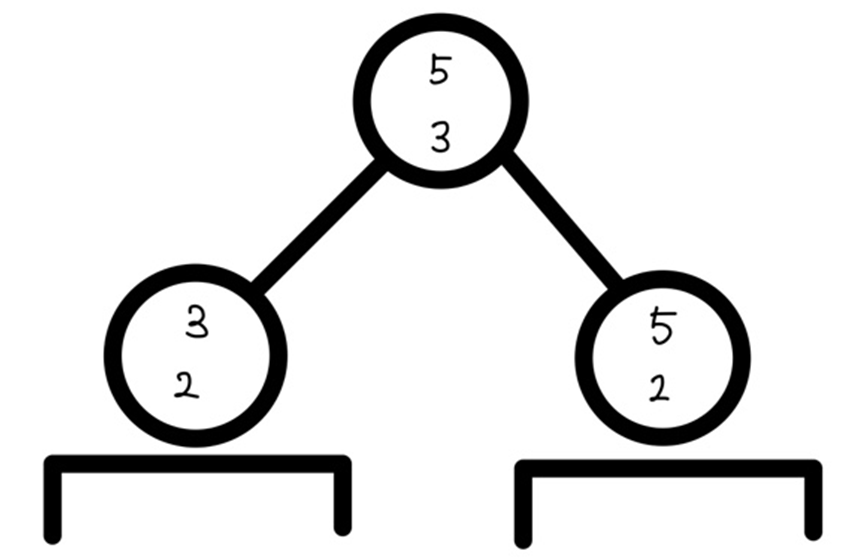
이러면 양쪽 구간에서 총 4개의 값을 가져오고, 이중 가장 큰 두개를 찾아오면 된다. 케이스를 크게 2가지로 나눠보자.

1. 한쪽 구간에서 최댓값 두개가 다 나오는 경우
2. 양쪽 구간에서 최댓값이 각각 하나씩 나오는 경우

어느 구간에서 전체구간의 최댓값이 나올지 모르기 때문에 최소 정보는 구간에 대한 최댓값 두개이다. 1번인 경우 한쪽의 노드가 그대로 올라가겠고 2번인 경우는 양쪽 노드에서 큰 값만 사용하면 되기 때문이다. 나는 이문제를 구조체를 이용한 트리로 풀었고, 위에 설명한 비효율적인 코드로도 통과는 되는것 같아 보인다.

 

다음 포스팅에서 세그먼트 트리의 유명한 또다른 응용에 대해서 알아보겠다.