티스토리 뷰
오일러 지표를 오랜만에 들었다.

위키 백과에 가보면 정의가 아주 복잡하고 엄밀한데 그렇게까지는 필요없고 3차원 폐곡면에 대해서만 생각해보자. 그럼 정의는 이렇게 된다.
$$\chi = v - e +f$$
여기서 $\chi$는 오일러 지표이고, $v$는 정점의 수, $e$는 모서리의 수, $f$는 면의 수이다. 구의 $\chi$는 $2$로 알려져있다. 따라서 구와 위상동형인 다면체들도 오일러 지표의 성질에 따라 $2$이다.
이걸 본 곳에서는 다면체가 아니고, 심지어 폐곡면도 아니었다. 부서진 다면체에 대해서 오일러 지표를 계산해야 하는 일이 있었다. 정확히는, 다면체 위의 어떤 면에서 시작해서 원하는 만큼 이 면과 연결되어있는 면을 떼어낸 괴상한 입체의 오일러 지표를 계산해야한다.
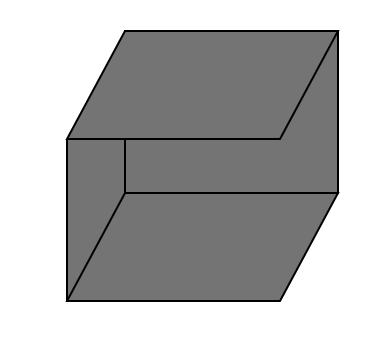
요건 육면체에서 면 두개를 뗀 모습이다. 이런 열린 모양의 오일러 지표는 어떨까? 위의 그림에서 계산해보면 정육면체에서 면이 두 개 없어지고 모서리가 하나 없어졌다. 그래서 $\chi =1$임을 알 수 있다. 일반화할 수 없을까? 당연히 할 수 있다. 진부하게 면이 어떻게 배치되어서 사이에 얼마나 많은 정점이 있고 얼마나 많은 선분이 있어서 이런건 넘어가자. 그런건 독자에게 연습문제로 남겨두겠다.
나의 개쩌는 증명 아이디어는 저 뻥 뚫린 공간을 곡면으로 채우는 것이다. 그럼 곡면과 평면이 합쳐진 괴랄한 입체가 하나 나오는데 이는 사실 구와 위상동형이다. 다르게 생각해보면 원래 다면체에 바람을 불어넣어서 모든 면을 곡면으로 만들고, 면을 들어낸다음 곡면으로 채우면 동일한 결과를 나타낸다. 좀 엄밀하지 않다는 생각이 들면 뚫린 부분의 점들을 한 평면 위로 모으는 것을 생각해보자. 위 그림에서는 육각형을 만들면 된다. 다른 점을 잘 옮기고 적절히 늘리면 모든 뚫린 면을 한 평면 위로 모을 수 있다.
이것도 역시 직관적으로 간단히 보일 수 있는데, 어떤 다면체의 삼각형이 아닌 면을 삼각형으로 분할한다고 생각해보자. 삼각형으로 나누거나 말거나 이 입체는 다면체이다. 그러므로 삼각형으로 나눈 입체 또한 $\chi = 2$를 만족한다. 그럼 이제부터는 자유다. 이 다면체를 아주 유동적인 클레이로 나무젓가락을 점으로 모은 구조물이라고 생각해보자. 아주 유동적인 클레이 때문에 힘을 주어서 정점에 모인 나무젓가락의 각도를 자유자재로 움직일 수 있다. 그럼 삼각형으로 분할하기 전의 다면체에서 들어낸 면을 동일하게 이 삼각형으로 분할한 입체에서도 들어낸다. 그리고 들어낸 면에 의해 연결 성분이 하나 이상 사라진 점들을 종이에 붙인다. 그러면 한 평면 위로 뚫린 부분이 온다. 그럼 이제 종이를 뒤집어서 나머지 젓가락들이 중력에 의해 알아서 늘어뜨려지도록 할 수 있을 것이다. 삼각형은 두 개씩 연결된 선분 3개가 있으면 자동결정되므로 이 입체의 모든 면은 2차원 평면위에 있음이 자명하다.
그래서 결론은 다면체에서 연결된 면을 원하는 개수만큼 들어낸 입체의 $\chi=1$이다. 엄밀하진 않지만 직관적으로 이걸 보일 수 있었다.
